Continuous Random Variable Example

For any continuous random variable with probability density function fx we have that. To construct a random Bernoulli variable for some.

Continuous Random Variable Definition Examples Explanation

Then X is a continuous rv.

. Lets look at an example. The normal random variable is a good starting point for continuous measurements that have a central value and become less common away from that mean. Financiers typically model stock prices and interest rates as continuous processes in continuous time.

For a continuous random variable the expectation is sometimes written as EgX Z x gx dFx. May be depth measurements at randomly chosen locations. Continuous uniform variables sometimes occur as the location of an event in time or space when the event is known to have happened on some fixed interval.

The Exponential Distribution Consider the rv Y with cdf FY y 0 y 0 1 ey y 0. Realizations of any random variable can be generated. Continuous-variable CV quantum information is the area of quantum information science that makes use of physical observables like the strength of an electromagnetic field whose numerical values belong to continuous intervals.

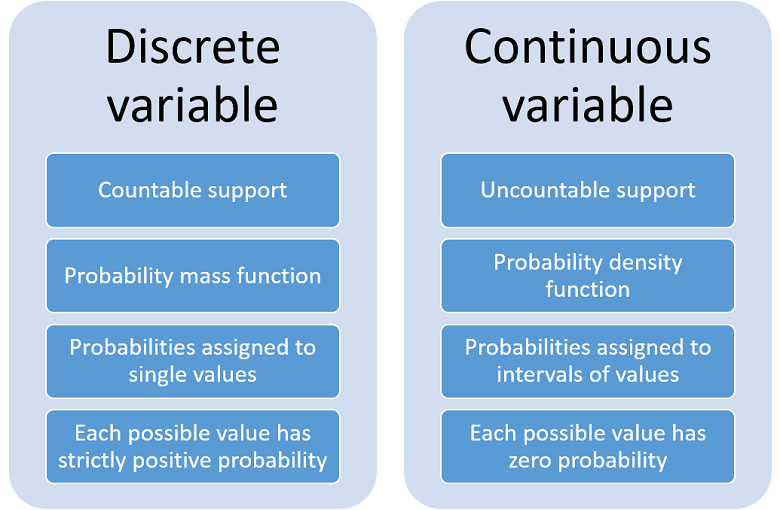
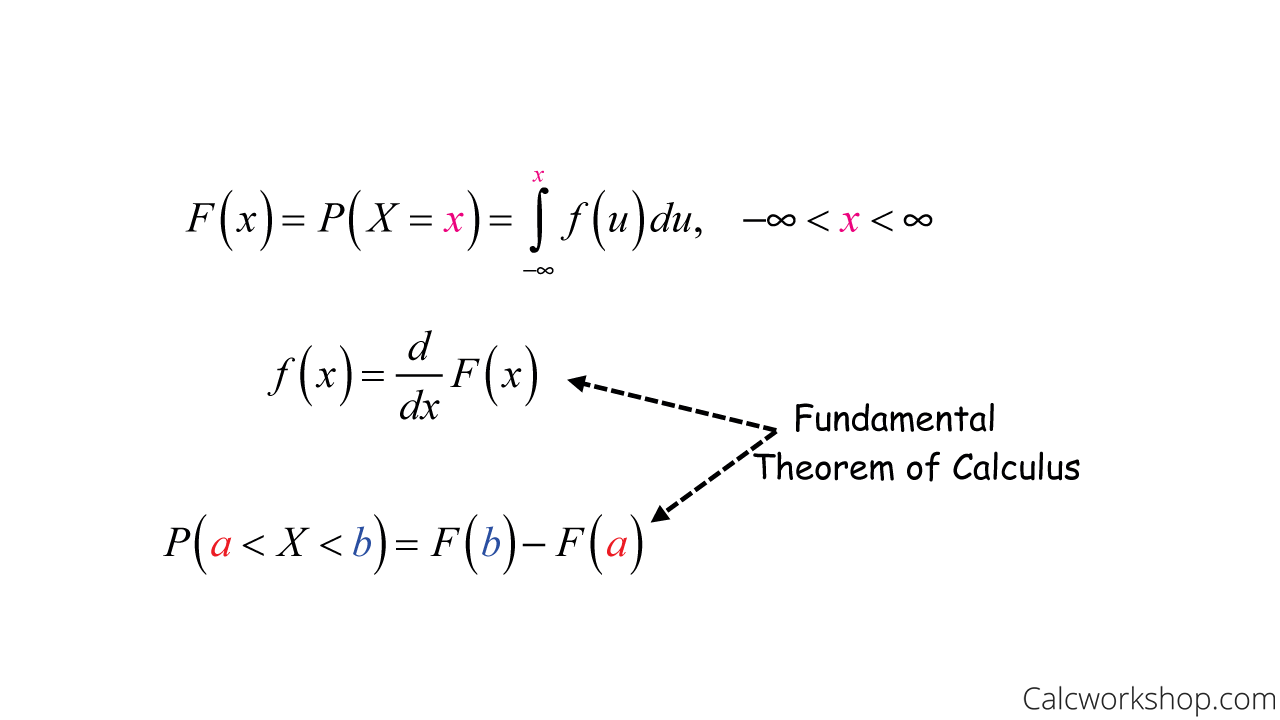
So if a variable can take an infinite and uncountable set of values then the variable is referred as a continuous variable. This meets all the requirements above and is not a step function. A continuous random variable is a random variable where the data can take infinitely many values.

Note that before differentiating the CDF we should check that the CDF is continuous. Working through examples of both discrete and continuous random variables. As we will see later the function of a continuous random variable might be a non-continuous random variable.

To go from a pdf to a pmf requires either a sampling and a normalization or an integration. Where Fx is the distribution function of X. Working through examples of both discrete and continuous random variables.

A variable which can only assume a countable number of real values ie the value of the discrete random sample is discrete in nature. But although the number 7211916 is a possible. This is not the case for a continuous random variable.

If buses run every 30 minutes without fail then the set of possible values of X is the interval denoted 030 the set of all decimal numbers between 0 and 30. In a continuous distribution the probability of getting exactly any of the discrete values is 0. A random variable can be categorized into two types.

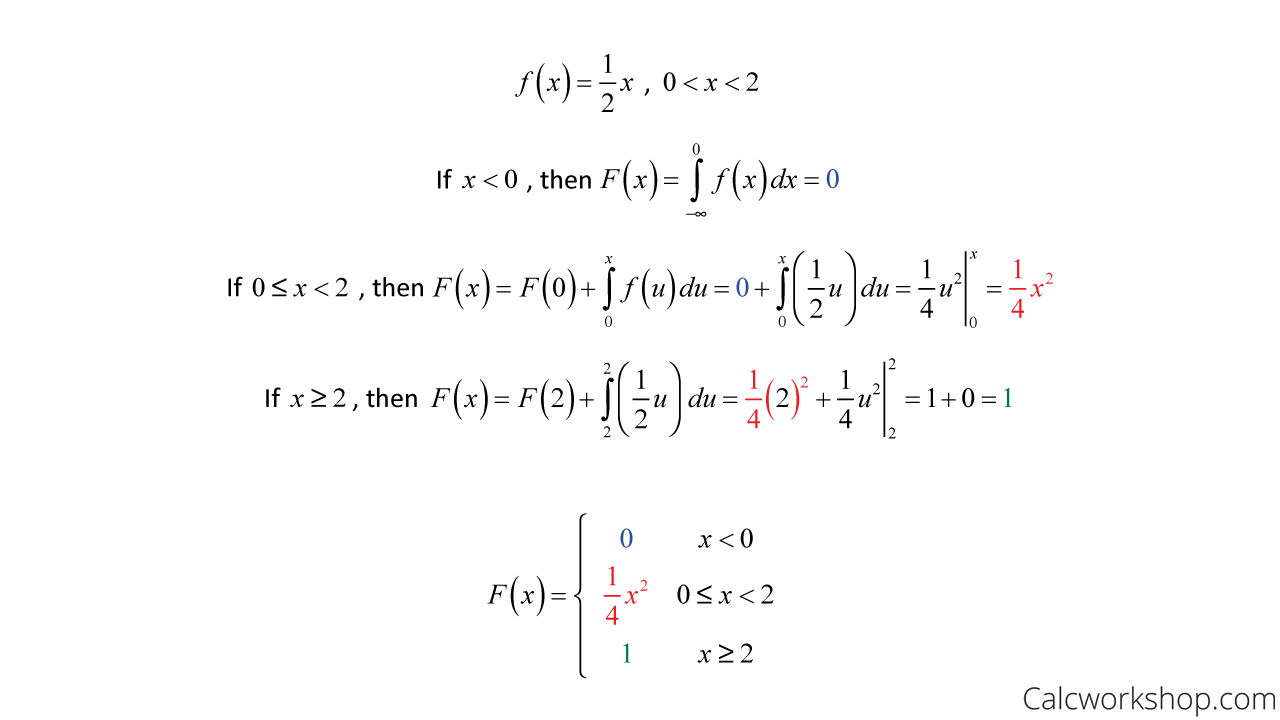
It is usually more straightforward to start from the CDF and then to find the PDF by taking the derivative of the CDF. But we also have random processes in continuous time where there is one random variable for each instant in time arranged as a continuum. If youre seeing this message it means were having trouble loading external resources on our.

Suppose 2 dice are rolled and the random variable X is used to represent the sum of the numbers. What is Random Variable in Statistics. An absolutely continuous random variable is a random variable whose probability distribution is absolutely continuous.

For example suppose X denotes the length of time a commuter just arriving at a bus stop has to wait for the next bus. Exponential variables show up when waiting for events to occur. A random variable is said to be continuous if its cdf is a continuous function see later.

If in the study of the ecology of a lake X the rv. Defining discrete and continuous random variables. For example suppose has a uniform distribution between 0 and 1.

Theorem 1 Expectation Let X. Then the smallest value of X will be equal to 2 which is a result of the outcomes 1 1 2 and the highest value would be 12 which is resulting from. Continuous variable as the name suggest is a random variable that assumes all the possible values in a continuum.

Random variables could be either discrete or continuous. The range for X is the minimum depth possible to the maximum depth possible. As the name suggests this variable is not connected or continuous.

A probability mass function is used to describe the probability distribution of a discrete random variable. In probability a real-valued function defined over the sample space of a random experiment is called a random variableThat is the values of the random variable correspond to the outcomes of the random experiment. Regardless it is wrong to use a continuous distribution for a discrete random variable.

Simply put it can take any value within the given range. For example a random variable measuring the time taken for something to be done is continuous since there are an infinite number of possible times that can be taken. Difference between random variable and random process For example we can.

Defining discrete and continuous random variables. One primary application is quantum computingIn a sense continuous-variable quantum computation is analog while quantum computation using. In particular the following theorem shows that expectation preserves the inequality and is a linear operator.

This is an important case which occurs frequently in practice. The value of the random variable depends on chance. A random variable X is continuous if possible values comprise either a single interval on the number line or a union of disjoint intervals.

First note that by the assumption beginequation nonumber f_YXyx left beginarrayl l frac12x quad -x leq y leq x quad. A continuous variable is one that is defined over an interval of values. The expectation operator has inherits its properties from those of summation and integral.

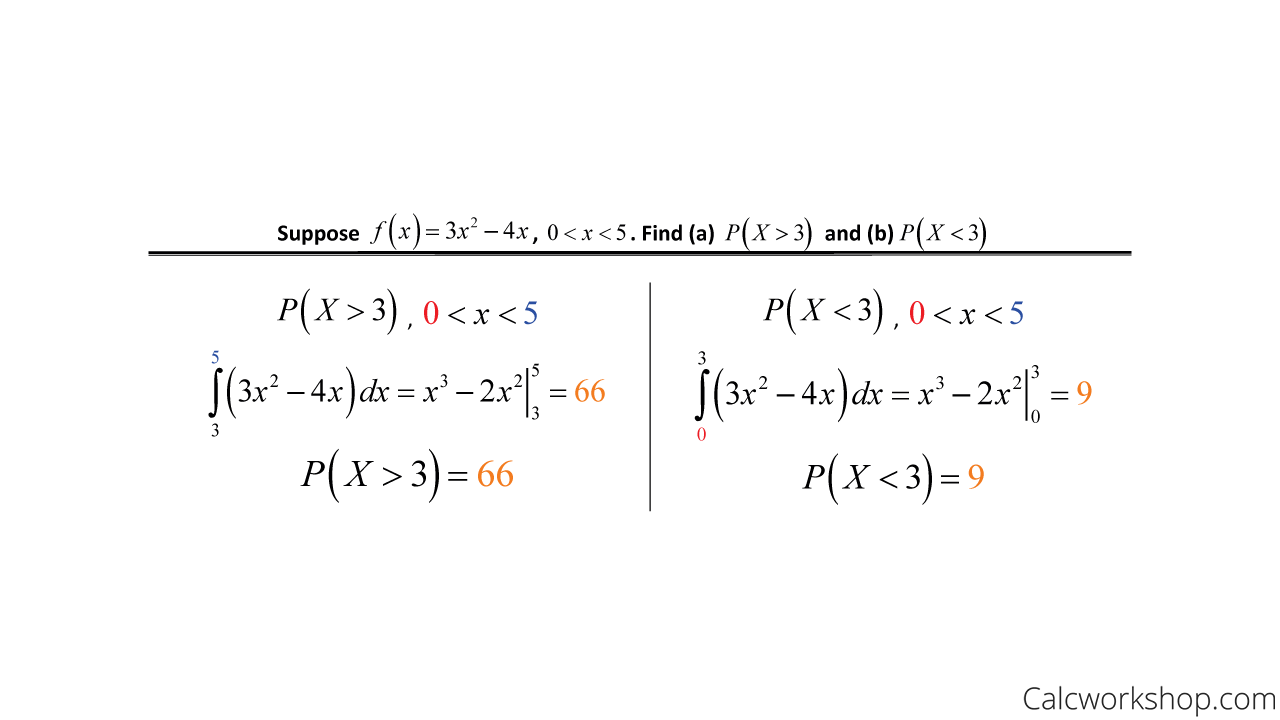
Continuous Random Variable Detailed W 7 Examples

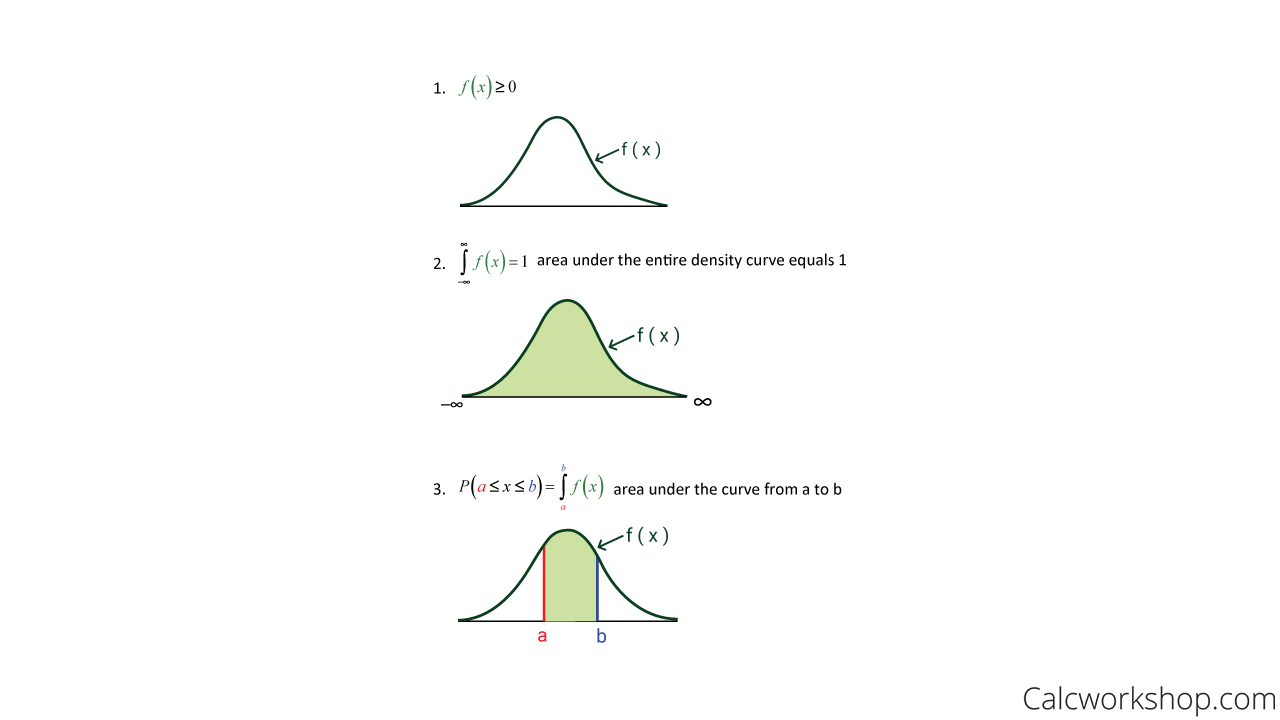
Continuous Random Variable Detailed W 7 Examples

Continuous Random Variable Detailed W 7 Examples

Continuous Random Variable Detailed W 7 Examples